3 Calibración

La calibración de un instrumento es una de las operaciones más frecuentes que realizamos en el laboratorio. No discutiremos los detalles de la calibración de cada una de las principales técnicas analíticas, sino que presentaremos una aproximación general válida, en principio, para todas.

En este texto discutiremos el modelo lineal de calibración.

Importante

En Estadística, un modelo lineal, en términos muy simples, es aquel en que sus parámetros son lineales. Es decir, podemos expresarlo en el caso univariado de la siguiente manera:

\[y = \beta_{0} + \beta_{1} x\] donde $\beta_{0}$ y $\beta_{1}$ es el intercepto y la pendiente, respectivamente. Por lo tanto, una calibración cuadrática sigue siendo “lineal” pues sus parámetros son lineales también:

\[y = \beta_{0} + \beta_{1} x + \beta_{2} x^{2}\] En cambio, un modelo de calibración de tipo exponencial no es lineal. Note que el parámetro $\beta_{1}$ está dentro del exponente:

\[y = \beta_{0} e^{\beta_{1}x}\]

En este texto, en pos de la simplicidad y por razones históricas, consideraremos una calibración cuadrática (o polinómica de cualquier grado) como no lineal. Es un abuso del lenguaje, pero todos los Químic@s entenderán a qué nos referimos.

3.1 Curva de calibración lineal

La calibración lineal es el modelo más utilizado en Química Analítica principalmente por su simpleza y, en algunos casos muy puntuales, porque tiene un soporte físico-químico que nos indica un comportamiento lineal entre la señal instrumental $y$ y las concentraciones de los calibrantes $x$.

Por ejemplo, en espectrofotometría la ecuación de Lambert-Beer dicta:

\[ \underbrace{A}_\text{y} = \underbrace{\epsilon \cdot b}_\text{$\beta_{1}$} \cdot \underbrace{C}_\text{x} \tag{3.1}\]

De la ecuación Equation 3.1 se observa claramente la relación con el modelo estándar de calibración lineal $y = \beta_{0} + \beta_{1}x$ asumiendo un intercepto $\beta_{0} = 0$.

Por lo tanto ¿por qué nos sorprende tanto encontrar un coeficiente de correlación alto en curvas de calibración espectrofotométricas? Era totalmente esperable, pues hay un modelo físico-químico que sustenta el modelo lineal.¹

\[y = \beta_{0} + \beta_{1} x + \epsilon \tag{3.2}\]

3.1.1 Diagnóstico de la calibración

Cuando hablamos de diagnóstico de la curva de calibración nos referiremos a evaluar las suposiciones estadísticas del modelo lineal Equation 3.2:

Normalidad de los residuos
Homocedasticidad
Independencia

Además, evaluaremos si el modelo lineal es adecuado para modelar nuestros datos de calibración.

Este diagnóstico no incorpora la evaluación metrológica de la curva, es decir, el control de calidad externo de la calibración utilizando, por ejemplo, una solución de control preparada independientemente a la curva.

3.1.2 ¿Cómo evaluar la linealidad?

3.1.2.1 Análisis de los residuos

3.1.2.2 Test de carencia de ajuste (Lack of fit)

3.1.2.3 Test de Mandel

3.1.3 ¿La curva pasa por el origen?

3.1.4 Incertidumbre de calibración lineal

Una vez que interpolamos la señal instrumental de la muestra problema $y_{0}$:

¿Cuál es la concentración de la muestra y su incertidumbre?

Para responder esta pregunta haremos uso directamente de la ecuación de incertidumbre de calibración lineal, que si bien es una aproximación, desde el punto de vista químico se cumple en la mayoría de los casos. Si desea conocer la ecuación exacta puede consultar…

Importante

Básicamente, esta incertidumbre sólo da cuenta del error aleatorio del instrumento (eje $y$) y no incorpora la incertidumbre de los calibrantes (eje $x$).

Si Ud. necesita incorporar la incertidumbre de los calibrantes, debe utilizar un modelo de regresión con error en ambos ejes.

A partir de la ecuación Equation 3.3 obtenemos la concentración de una muestra problema $x_{0}$ cuya señal instrumental es $y_{0}$:

\[ x_{0} = \frac{y_{0} - \beta_{0}}{\beta_{1}} \tag{3.3}\]

Si aplicáramos la guía GUM para obtener la incertidumbre estándar de calibración $u(x_{0})$ sería algebraicamente bastante engorroso, pues hay unas covarianzas no muy amistosas entre pendiente e intercepto. Afortunadamente $u(x_{0})$ puede aproximarse muy bien a través de la ecuación Equation 3.4:

\[ u(x_{0}) = \frac{\sigma_{y/x}}{\beta_{1}} \sqrt{\frac{1}{n} + \frac{1}{m_{0}} + \frac{(x_{0} - \overline{x})^2} {\sum_{i}^{n} (x_{i} - \overline{x})^2}} \tag{3.4}\]

donde:

$\sigma_{y/x}$ es la desviación estándar del error aleatorio $\epsilon$
$n$ es el número de calibrantes
$m_{0}$ es el número de replicados independientes de la muestra problema
$\overline{x}$ es el promedio de la concentraciones de los calibrantes
$\beta_{1}$ es la pendiente

Antes de proseguir, mirando la ecuación anterior ¿cómo podríamos minimizar esta incertidumbre?:

Para minimizar una fracción $\frac{a}{b}$:

aumentamos el denominador $\boldsymbol{b}$ o bien disminuimos el numerador $\boldsymbol{a}$

aumentando el número de calibrantes $n$
aumentando el número de replicados de la muestra problema $m_{0}$
diseñando la curva de tal manera que la concentración de la muestra problema $x_{0}$ se ubique en el centro de la curva $\overline{x}$. De esta forma, si $x_{0} = \overline{x}$, entonces:

$\left(x_{0} - \overline{x}\right)^2 = 0$
el denominador del tercer término de la raíz no es fácil de visualizar $\sum_{i}^{n} (x_{i} - \overline{x})^2$. Lo que está indicando es lo siguiente:
- Calcule el promedio de las concentraciones de los calibrantes $\overline{x}$
- A cada concentración $x_{i}$ réstele el promedio $\overline{x}$
- A cada diferencia elévela al cuadrado
- Sume todas las diferencias al cuadrado
¿cómo aumentamos este término?
- utilizando todo el rango lineal, pues agrandamos la distancia $(x_{i} - \overline{x})^2$
- también aumentando el número de calibrantes $n$
- ¡atención! recomendación anti-intuitiva: ubicando los calibrantes en los dos puntos extremos de la curva y niguno entremedio de ellos. Es decir, si prepara $n = 6$ estándares, ubique 3 en la concentración más baja y los otros 3 en la más alta. Lo sé, nadie haría eso, pero si ya demostró la linealidad de la curva de calibración, la Estadística predice que es una forma de minimizar esta incertidumbre.
En relación a minimizar $\sigma_{y/x}$ no hay mucho que hacer pues es una característica intrínseca de su instrumento. La únicas recomendaciones serían:
- una adecuada mantención del equipo de tal forma de tener una buena repetibilidad de la señal instrumental
- calibrar el material de vidrio utilizado en la preparación de los calibrantes
- preparación gravimétrica de las soluciones de calibración. Por lo tanto, su gráfico de calibración tendrá de unidades de masa/masa en el eje $X$ (por ej: mg/kg). Esto da para una larga y profunda discusión metrológica.
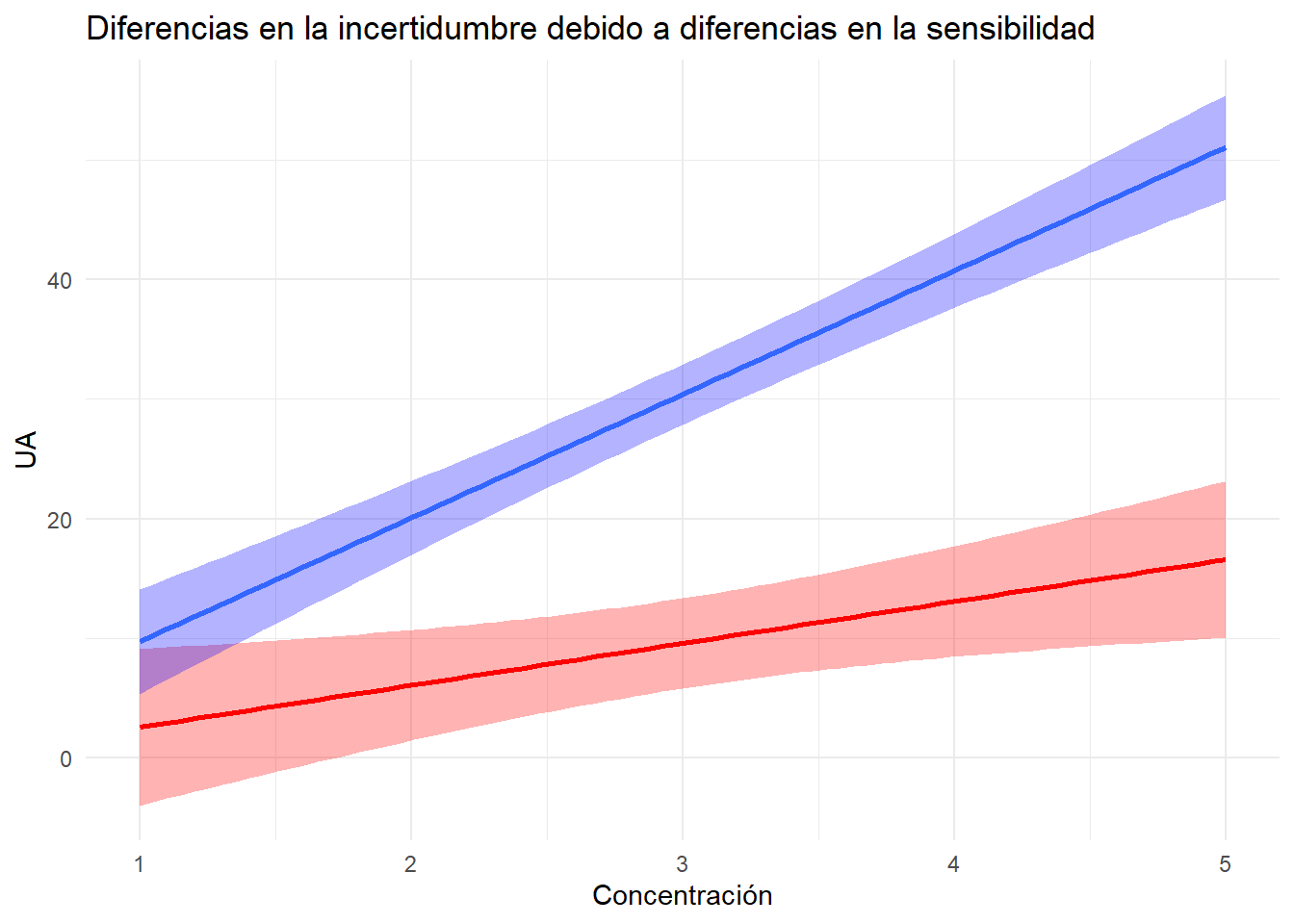
Con la pendiente de la curva de calibración, bajo condiciones fijas de medición del instrumento, tampoco hay mucho que podamos hacer, pues también es característica de la configuración instrumental. De la ecuación Equation 3.3 podemos entender por qué se prefieren métodos instrumentales con mayor sensibilidad (mayor pendiente $\uparrow \beta_{1}$). En la figura Figure 3.1 se puede visualizar el efecto de aumentar la sensibilidad instrumental. La curva azul tiene una pendiente de calibración (sensibilidad) 3 veces mayor que la curva roja. Note las diferencias en el ancho de las bandas de incertidumbre de calibración.

Figure 3.1: Comparación de incertidumbres de calibración

3.1.4.1 ¿Cómo se interpreta la incertidumbre de calibración?

Recordemos que en el modelo de calibración lineal Equation 3.2 la incertidumbre de calibración Equation 3.4 sólo incorpora la incertidumbre del instrumento (eje $Y$), pues asume que los calibrantes son tienen incertidumbre (eje $X$).

Bajo este modelo, imagine que inyectamos los calibrantes en el equipo, obtenemos la lectura instrumental para cada uno y ajustamos la curva de regresión lineal. Ahora, repita esta operación unas 1000 veces, es decir, obtendrá 1000 curvas de calibración.

Recuerde: Son los mismos calibrantes que han sido inyectados 1000 veces. Cada vez se ha obtenido una curva de calibración con inetercepto y pendiente distintos debido a la variabilidad instrumental.

La figura Figure 3.2 muestra las 1000 curvas de calibración ajustadas:

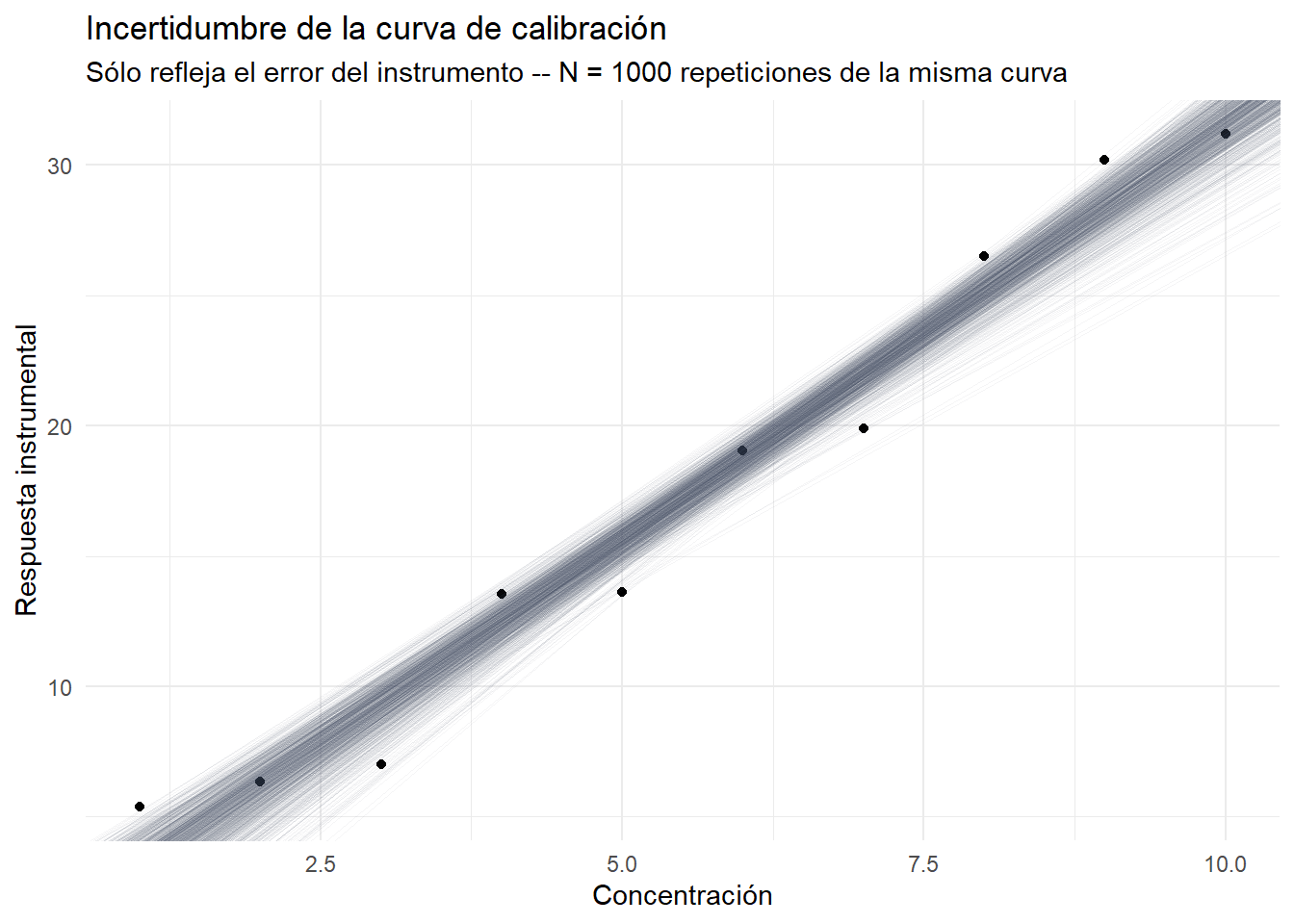
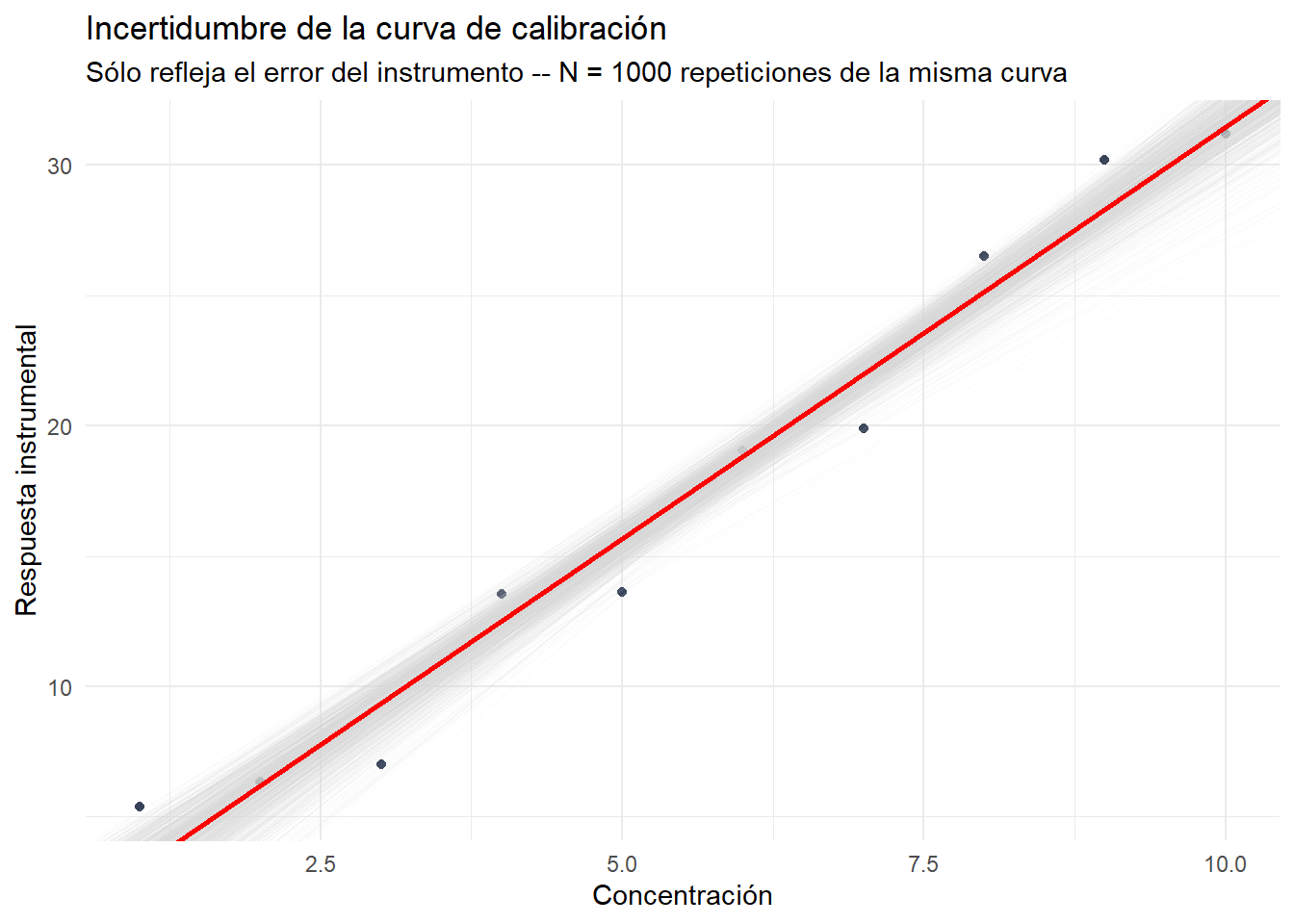
Los puntos que observa en la figura corresponden a la curva de calibración inicial. De las infinitas curvas que Ud. pudo haber obtenido, ha calculado la concentración de la muestra con la primera calibración (es decir, la que Ud. obtiene en el laboratorio). Si Ud. repitiera el experimento de cuantificación, es decir, leyera de nuevo los calibrantes, obtendría otra concentración debido a que obtendría diferente pendiente e intercepto, pues siempre habrá variabilidad en las lecturas (no en los calibrantes). La figura Figure 3.3 describe este proceso.

3.1.5 Simulación de una curva de calibración

Para entender qué ocurre estadísticamente cuando calibramos un equipo, llevaremos a cabo una simulación de una curva de calibración lineal de acuerdo al modelo Equation 3.2:

\[y = \beta_{0} + \beta_{1} x + \epsilon\]

La “gracia” de simular una calibración es que conocemos de antemano qué es lo que esperamos de la simulación:

sabemos cuáles son sus parámetros (pendiente e intercepto)
cuál es el error de calibración
si es homocedástico (mismo error de calibración en todo el rango lineal)
si pasa por el origen (intercepto = 0)
dónde esperamos la menor incertidumbre de calibración
sabemos que SÍ ES LINEAL
sus residuos SON NORMALES
etc.

Es decir, es una curva de calibración perfecta desde el punto de vista de las suposiciones del modelo, porque así la hemos simulado.

¿Qué necesitamos definir para simular una calibración lineal?

el número de calibrantes $n$
las concentraciones $x$
el intercepto $\beta_{0}$
la pendiente $\beta_{1}$
el error de calibración $\sigma_{y/x}$
si la curva es homocedástica o no (es decir, $\sigma_{y/x}$ constante)

El siguiente código en R simula una curva de calibración con todos los parámetros definidos:

set.seed(123)       # para reproducir la simulación (opcional)
n <- 10             # número de calibrantes
x <- 1:n            # concentraciones [ppm]
e <- rnorm(n, 0, 1) # error aleatorio normal con media 0 y varianza cte
b0 <- 0             # intercepto
b1 <- 3             # pendiente
y <- b0 + b1*x + e  # absorbancias

La figura ?fig-cal.sim muestra la curva de calibración

Ajustamos el modelo lineal:

fit.lineal <- lm(y ~ x)
summary(fit.lineal)


Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.1348 -0.5624 -0.1393  0.3854  1.6814 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.5255     0.6673   0.787    0.454    
x             2.9180     0.1075  27.134 3.67e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9768 on 8 degrees of freedom
Multiple R-squared:  0.9893,    Adjusted R-squared:  0.9879 
F-statistic: 736.3 on 1 and 8 DF,  p-value: 3.666e-09

3.2 Calibración lineal ponderada

En el modelo de calibración lineal Equation 3.2 asumimos que el error del instrumento es constante en todo el rango de concentración, propiedad que se denomina homocedasticidad. Estadísticamente, esto implica que el el error aleatorio $\epsilon$ tiene una varianza $\sigma_{y/x}^{2}$ constante.

Corroboramos la suposición de homocedasticidad con un gráfico de residuos y, específicamente, con el test de Breusch-Pagan del package lmtest::bptest.

Es muy frecuente en Química Analítica obtener calibraciones heterocedásticas, es decir, cuando el error en el eje $Y$ $\sigma_{y/x}$ no es constante. La figura Figure 3.4 muestra una curva de calibración que presenta heterocedasticidad.

Nota

La heterocedasticidad no es un problema de la curva de calibración, un error en la lectura o en la preparación de los calibrantes (asumiendo que todos los QC de calibración están OK).

Es una característica del sistema de medición instrumental que debe abordarse adecuadamente, nada más.

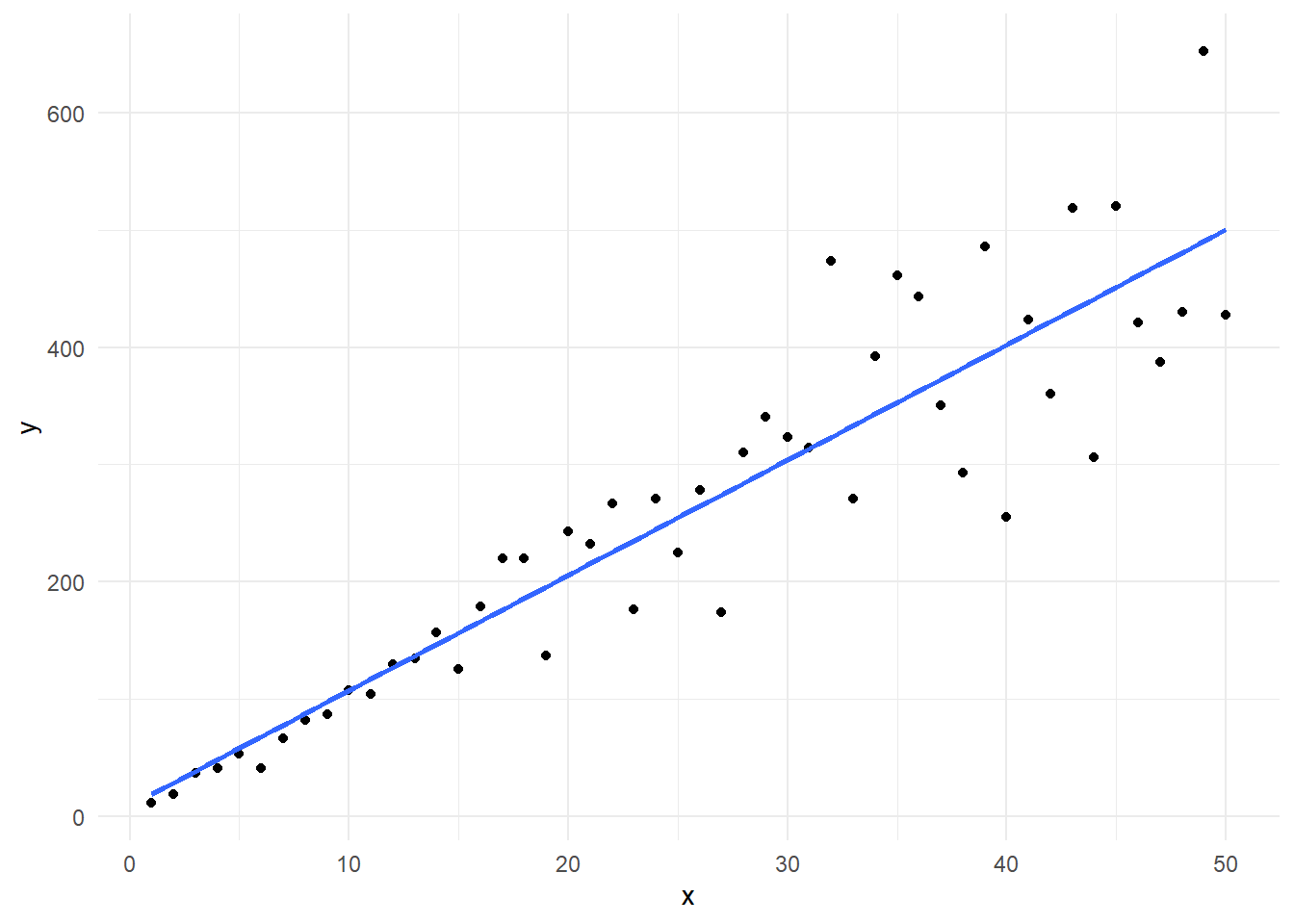
Puede que la heterocedasticidad no sea evidente en la curva de calibración, sin embargo, el análisis de residuos es elocuente: a medida que aumenta la concentración, aumenta la variabilidad de los residuos.

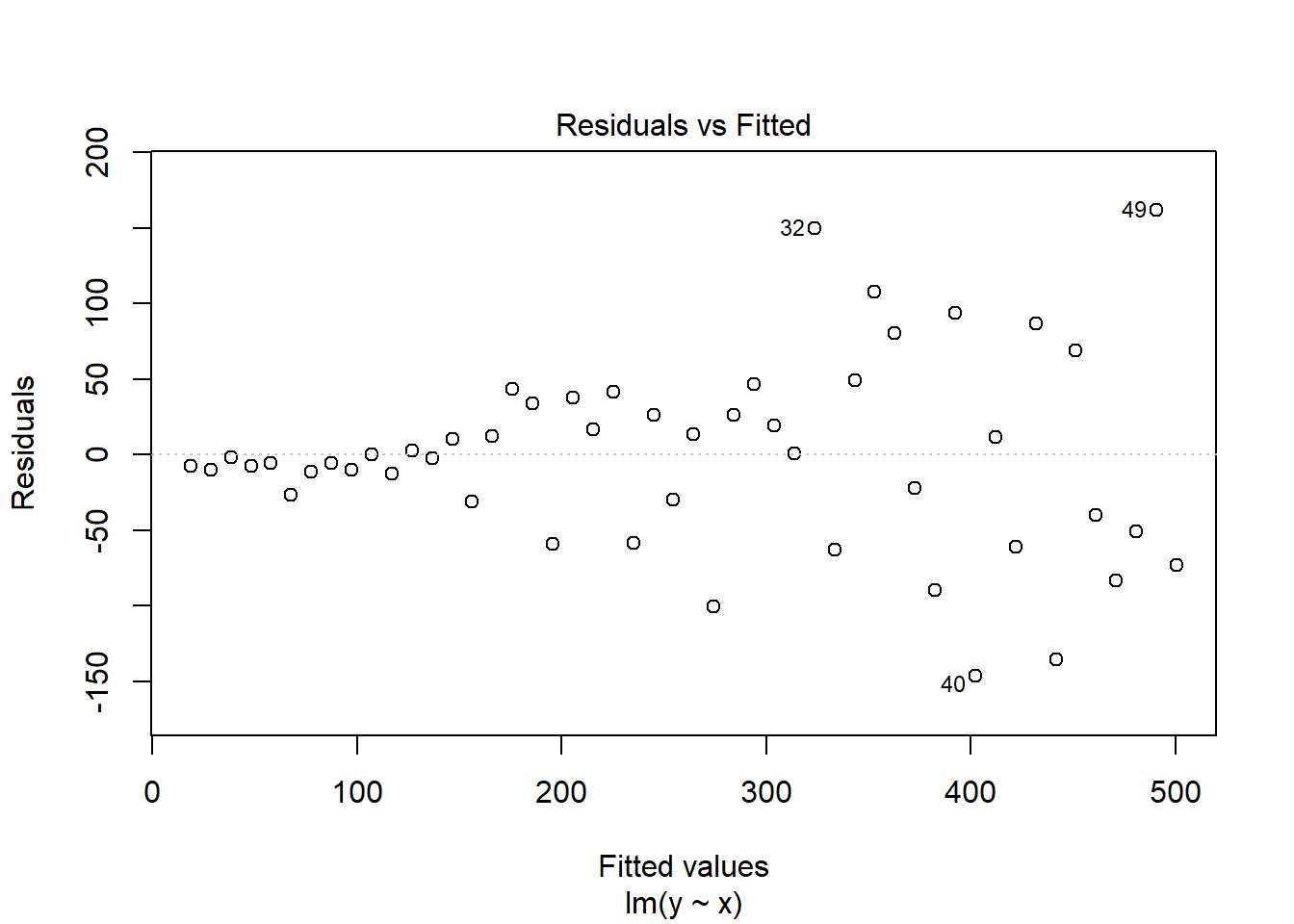
¿Cuál es problema de no abordar la heterocedasticidad?

3.3 Curva de calibración no lineal

3.3.1 ¿Es razonable el modelo de calibración?

3.3.2 Incertidumbre de calibración no lineal

3.3.3 Simulación de una curva de calibración no lineal

OK, de acuerdo. Este modelo físico-químico sólo es válido bajo ciertas condiciones (como todos los modelos), de hecho son conocidas las desviaciones de la ley de Lambert-Beer a altas y bajas concentraciones.↩︎